Die N.E.R.D.-Aufgabe für den Monat Oktober 2021! Lösung!

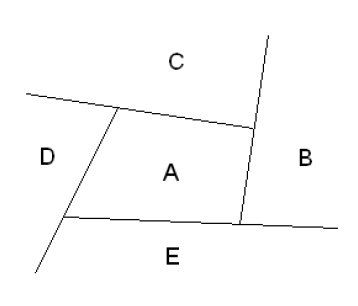
Die in der Grafik zu sehenden Gebiete A, B, C, D und E sollen so gefärbt werden,
dass benachbarte Gebiete verschiedene Farben haben. Auf wie viele Arten kann
man dies tun, wenn man
a) 4 verschiedene Farben zur Auswahl hat?
b) 5 verschiedene Farben zur Auswahl hat?
c) n verschiedene Farben zur Auswahl hat?
Hinweis: Es ist nicht erforderlich, alle Farben zu benutzen.
Wer möchte, kann mir seine Überlegungen per Mail schicken.
Wie immer gibt es neben Ruhm und Ehre viele N.E.R.D.-Punkte zu ergattern.
Lösung
A, B und C können auf n untere Faktorielle 3 = n(n-1)(n-2)= n!/(n-3)! Arten eingefärbt werden. Dann muss man zwei Fälle unterscheiden.
i) Hat D dieselbe Farbe wie B, so hat E (n-3) verbleibende Farben + die Farbe von C zur Verfügung, also insgesamt (n-2).
ii) hat D eine andere Farbe als B, so hat D (n-3) Möglichkeiten und E (n-4+1), also ebenfalls (n-3). Daraus ergeben sich (n-3)2 Kombinationen.
Insgesamt erhalten wir also für die Zahl der Färbungen
n!/(n-3)!(n-2+(n-3)2) = (n3-3n2+2n)(n2-5n+7)= n5-8n4+24n3-31n2+14n
Setzen wir n=4, so erhalten wir 72 Möglichkeiten, für n=5 sind es 420.






